Answer:
Option A,B,C
Explanation:
Note: This question can be solved if the right-hand side chamber is assumed to open so that its pressure remains constant even if the piston shifts towards night.
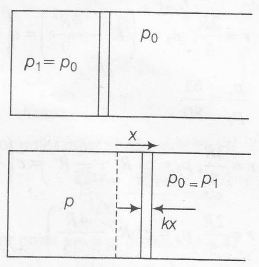
(a) pV=n RT \Rightarrow p \propto\frac{T}{V}
Temperature is made three times and volume is doubled
\Rightarrow p_{2}=\frac{3}{2}p_{1}
Further x=\frac{\triangle V}{A}=\frac{V_{2}-V_{1}}{A}
=\frac{2V_{1}-V_{1}}{A}=\frac{V_{1}}{A}
p_{2}=\frac{3p_{1}}{2}=p_{1}+\frac{kx}{A}
\Rightarrow KX=\frac{P_{1}A}{2}
Energy of spring
\frac{1}{2}kx^{2}=\frac{p_{1}A}{4}x=\frac{p_{1}V_{1}}{4}
(b) \triangle U=nc_{v}\triangle T=n\left( \frac{3}{2}R\right) \triangle T
= \frac{3}{2}(p_{2}V_{2}-p_{1}V_{1})
\frac{3}{2}\left[ \left(\frac{3}{2}P_{1}\right) (2V_{1})-p_{1}V_{1}\right]=3p_{1}V_{1}
(c) p_{2}=\frac{4p_{1}}{3}\Rightarrow p_{2}=\frac{4}{3}p_{1}=p_{1}+\frac{kx}{A}
\Rightarrow kx=\frac{p_{1}A}{3}\Rightarrow x=\frac{\triangle V}{A}=\frac{2V_{1}}{A}
W_{gas}=(p_{0}\triangle V +W_{spring})
=(p_{1}Ax+\frac{1}{2}kx.x)
=+\left( p_{1}A.\frac{2V_{1}}{A}+\frac{1}{2}.\frac{p_{1}A}{3}.\frac{2V_{1}}{A}\right)
=2p_{1}V_{1}+\frac{p_{1}V_{1}}{3}=\frac{7p_{1}V_{1}}{3}
(d)
\triangle Q=W+\triangle U
= \frac{7p_{1}V_{1}}{3}+\frac{3}{2}\left( p_{2}V_{2}-p_{1}V_{1}\right)
= \frac{7p_{1}V_{1}}{3}+\frac{3}{2}\left(\frac{4}{3}p_{1}.3V_{1}-p_{1}V_{1} \right)
= \frac{7p_{1}V_{1}}{3}+\frac{9}{2}p_{1}V_{1} =\frac{41p_{1}V_{1}}{6}
Note: \triangle U=\frac{3}{2}(p_{2}V_{2}-p_{1}V_{1}) , has been obtained in part (b).